Safe from the Losing Fight

Something any serious vector graphics application has to implement is boolean operations. Boolean operations allow the user to combine bezier paths in interesting and powerful ways to create new shapes. The four common ones are:

Operation	Example
(None)
Union (Logical Or)
Intersect (Logical And)
Difference
Join (Exclusive Or)

Implementing them is somewhat involved, so I’m breaking the explanation up into two articles. This post will focus on finding intersections between individual bezier curves, and the next will show how to implement the boolean operations based on that. The algorithm presented will be able to handle arbitrary closed bezier paths, including those with holes and self intersections.

If you’re impatient, you can skip straight to the commented source code. As usual, I’ve released it under the MIT license. I encourage you to play with the sample application to see what it can do.

Clipping until it converges

This post I’m focusing on finding intersections between individual bezier curves using an algorithm called bezier clipping. It’s described in the paper “Curve intersection using Bezier clipping” by TW Sederberg and T Nishita. If you’re following along in the source code, it’s implemented in the FBBezierCurve class.

The first thing to realize is that finding intersections between curves isn’t exact. I won’t be able to plug the inputs into a formula and get back all the points where the curves intersect. Instead, I’ll iteratively whittle down the curves to ranges that could possibly intersect until I get down to a point or eliminate the curve entirely.

So the pseudocode for the main loop would be:

FBBezierCurve *us = ...; // passed in
FBBezierCurve *them = ...; // passed in
FBRange usRange = FBRangeMake(0, 1);
FBRange themRange = FBRangeMake(0, 1);
while ( !FBRangeHasConverged(usRange) && !FBRangeHasConverged(themRange) ) {
	BOOL intersects = NO;
	us = [us bezierClipWithBezierCurve:them range:&usRange intersects:&intersects];
	if ( !intersects )
		return; // no intersections
	them = [them bezierClipWithBezierCurve:us range:&themRange intersects:&intersects];
	if ( !intersects )
		return; // no intersections
}

Here a FBBezierCurve is one cubic bezier curve, as defined by two end points and two control points. FBRange is a parameter range defined by a minimum and maximum. A parameter value falls between [0..1] and is used for the parametric form of a bezier curve. In my case it keeps track of the range of the curve that could possibly intersect with the other curve.

The method bezierClipWithBezierCurve: refines the range passed in by determining the range where self could intersect with the curve passed in. It can also determine if there is no range where the two curves intersect. Don’t worry about how this is done right now, I’ll explain it later.

Each time through the loop I clip each curve a bit more, refining the range where the two curves might possibly intersect. The refined range is fed into the next iteration of the loop, which refines it a bit more. This continues until the minimum and maximum values of the range are close enough to be satisfactory (in my implementation, six decimal places). It’s also possible I discover, in clipping one curve against the other, that they don’t intersect at all. In that case, I can stop there.

The pseudocode above handles the common case where there is one (or no) intersection between the two curves. However cubic bezier curves can intersect up to nine times, so I need a way to detect when there are multiple intersections, and a way to find them. Detecting the possibility is easy; each time through the loop I compute how much I’ve reduced the intersection ranges by. If it’s less than 20%, then it’s likely there are multiple intersections, which would prevent the range from converging quickly.

Once I detect that I might have multiple intersections, I look at which range (and thus curve) is bigger. I split the correspond curve in half. I then recurse: for each of the halves I find the intersections between it and the other full curve. I take the combined results and return.

If you want to see the main loop in all it’s excruciating detail, check out the commented intersectionsWithBezierCurve:usRange:themRange:originalUs:originalThem: method. There are some implementation details I didn’t cover here, but are explained in the comments.

Fat Lines

In the previous section I glossed over how I can refine the range of a curve that could possibly intersect with the other curve. I’ll tackle how to do that now.

What I really need is a way to more simply represent the area a given bezier curve could possibly inhabit. Once I have that I can determine which parts of the other bezier lie inside of that area (and thus possibly intersect), and which don’t.

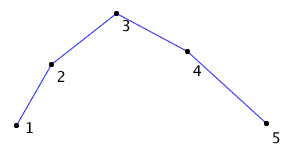
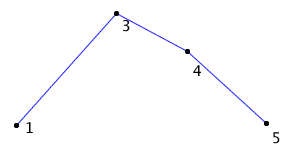
To this end, Sederberg and Nishita introduce the concept of a fat line. A fat line is a line through the end points of the bezier curve, but fat enough it encloses the entire curve.

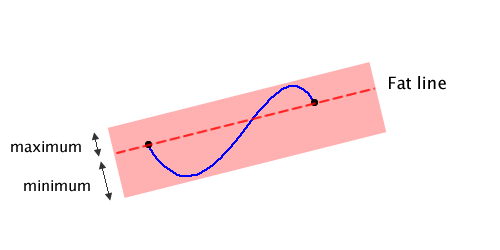
Above you can see the bezier curve in blue and the fat line in the pink color, crossing through the curve’s end points. In code, the fat line is represented by a line (the dashed line above), plus two signed distances describing how far to extend the fat line above and below the dashed line. (Signed distance just means the value is negative if it falls below the line, positive if above.) The two distances form the bounds of the fat line, and are called the minimum and maximum bounds.

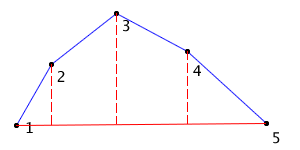
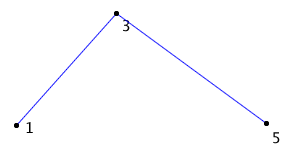
Computing an approximation to the minimum and maximum bounds is straightforward if I take advantage of the convex hull property. The convex hull is the polygon formed by connecting the end and control points with line segments. The convex hull property states that the polygon will completely enclose the bezier curve, as you can see below. The curve is in blue and the convex hull in red.

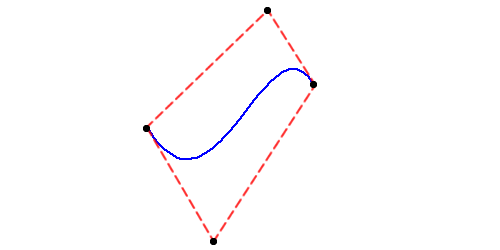
So to compute the minimum and maximum bounds, I just compute the signed distances of the end and control points from the dashed line and chose the minimum and maximum distances.

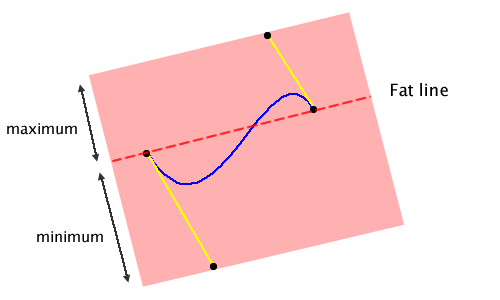
As you can see, using the convex hull to compute the minimum and maximum bounds doesn’t produce optimal results (i.e. the fat line fits loosely around the curve, not tightly). However the approximate bounds are cheap to compute and are good enough for my purposes.

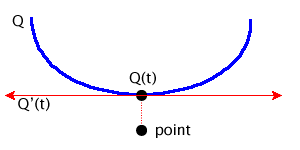
Based on the fat line, it’s easy to see if any given point could possibly intersect with the bezier curve. Simply compute the signed distance from the line to the point. If that signed distance lies inside the fat line bounds, then it could intersect. If not, then it definitely doesn’t intersect.

Bezier clipping

I’ve simplified the clipping curve to a fat line and bounds, and can use it to see if a point could lie inside the clipping curve. Next I need to clip the subject bezier curve with the fat line.

The above diagram shows a range on the subject bezier that falls inside of the fat line, and thus could intersect with the other bezier. The piece inside the fat line is the bezier curve I want to end up with.

I start by calculating the signed distances of the end and control points of the subject bezier to the fat line. Next I construct a bezier curve from these distances, like so:

NSPoint endPoint1 = NSMakePoint(0, distance(fatline, subjectCurve.endPoint1));
NSPoint controlPoint1 = NSMakePoint(1.0/3.0, distance(fatline, subjectCurve.controlPoint1));
NSPoint controlPoint2 = NSMakePoint(2.0/3.0, distance(fatline, subjectCurve.controlPoint2));
NSPoint endPoint2 = NSMakePoint(1, distance(fatline, subjectCurve.endPoint2));

I spread the distance bezier points out evenly between 0.0 and 1.0 on the X axis, and use the distances from the fat line as Y values. By uniformly spreading the X values out, they will correspond to parameter values for the parametric form of the subject bezier.

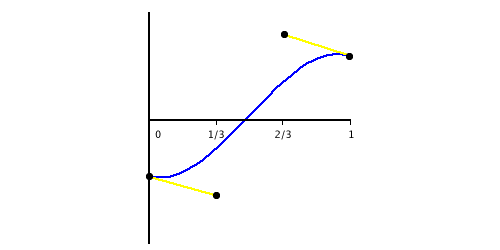
Since the Y axis is the distance from the fat line, I can just throw the fat line bounds on the graph.

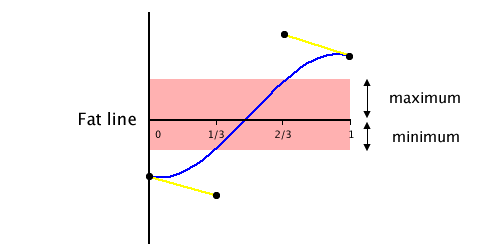
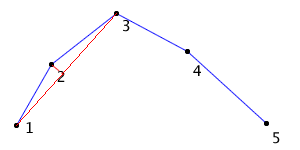
If I can calculate the X values of where the distance bezier crosses the minimum and maximum bounds, then I’ll have the range of the subject bezier that falls inside the fat line. To do that, I’ll once again rely on the convex hull property.

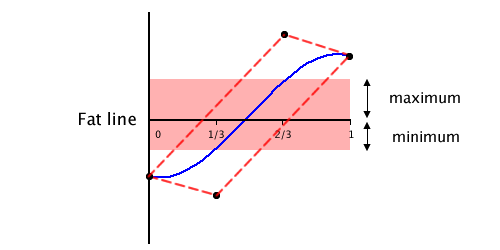
In the above diagram, the convex hull is the dashed red line. Computing the intersection of two lines is easy, so I find the intersections of the convex hull with the horizontal minimum and maximum lines. The lowest and highest X values define the parameter range on the subject bezier curve that fall into the fat line bounds, and thus could intersect the other curve.

There are two special cases here, both occurring when the distance bezier doesn’t intersect with the minimum or maximum fat line bounds. If the distance bezier falls completely inside the fat line bounds, then I can’t whittle the subject bezier down any, and I’m forced to return the entire subject bezier untouched. If the distance bezier lies completely outside the fat line bounds, I know the two curves don’t intersect, and return that.

If I did successfully refine the possible intersecting range, I need to cut down the subject curve to match. Fortunately, de Casteljau’s algorithm makes it easy to split bezier curves at a specific parameter value. See the BezierWithPoints() helper function for the implementation of that algorithm.

That completes how to clip one bezier curve against another. To summarize: compute a fat line and bounds from the clipping bezier, compute a distance bezier from the other curve, and see where the distance bezier’s convex hull intersects the fat line bounds. Using the intersections’ x values as the parameter range where the curves could intersect, cut the subject bezier down to match the range.

Points of interest

Although the above description presents the complete algorithm for finding intersections between two bezier curves, I wanted to point out a couple of other things. These are implementations details that I either found interesting and/or difficult.

1. After the main intersection loop (in intersectionsWithBezierCurve:usRange:themRange:originalUs:originalThem:) there’s a bit of code that checks to see if both curves have converged to a point. The loop bails as soon as one curve converges since the math for clipping falls apart as soon as one curve becomes a point. However for implementing the boolean operations, I need good parameter values for both curves. Since I know the 2D intersection point from the curve that converged, and I can guess a reasonable parameter value for the curve that didn’t, I can use Newton’s method to refine the parameter value of the curve that didn’t converge. Fortunately, that’s something I’ve done before when fitting curves to points.

2. In the method that clips one bezier curve against the other (bezierClipWithBezierCurve:original:rangeOfOriginal:intersects:) you’ll notice that I don’t compute and clip against one fat line, but two. The second fat line is perpendicular to the regular one:

   

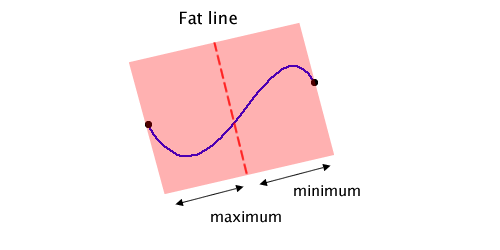
   Most of the time the regular fat line will clip out more of the curve than the perpendicular one. However, clipping against the perpendicular fat line does help the possible intersection range converge more quickly.

3. I mention the convex hull a couple of times, but gloss over how to build it. It is made up of just the end and control points, but the order is important, and sometimes points need to be removed if they’re collinear. There are several algorithms to build the convex hull, but Graham Scan is supposedly the best for 2D curves. It took me a few tries to get it right. Not all of the reference implementations/descriptions that I found covered the edges cases, such as what to do when I encountered collinear points. The best I found ended up being this one.

   Check out the convexHull method for my implementation.

Conclusion

Although I’m finding bezier curve intersections for the purpose of performing boolean operations, it can be used for other applications as well. Heck if I know what those are though. So next time I’ll dive into implementing union, intersect, difference, and join.

Be sure to enjoy the complimentary source code in the mean time.

Since I’ve previously written about how to implement a basic bitmap brush I thought it would be fun to figure out how to build a vector brush, like what you would find in Adobe Illustrator or Fireworks. A vector brush works the same as a bitmap brush from the viewpoint of the user, except that the resulting brushing stroke is scalable and otherwise editable after it is made. That’s because the resulting brush stroke ends up being a bezier path. In this post, I’ll show how it’s done.

If you’re impatient, you can always skip to the source code. It is licensed under the MIT license.

Naive Implementation

The direct way to implement the vector brush would be to simply record the mouse movements into a NSBezierPath. On a mouse down, create an NSBezierPath, do a move to the first point, then on subsequent mouse drags add line to’s to the NSBezierPath. Since I already have an NSBezierPath now, I can just draw it to represent the brush stroke. If you run the sample application with all the options under the Options menu (Show Points, Simplify Path, and Fit Curve) turned off, it’ll do exactly that. A brush stroke will look something like:

That actually doesn’t look bad. Does that mean I’m done? To answer myself, I’ll turn on the Show Points option under the Options menu:

Show Points draws an orange, hollow square around each of the points that make up the path. As you can see, there are a ton of them, about 160 in this case. Having that many points means editing the path afterwards is going to be rather difficult. Also, I can see that most of the points are redundant; they aren’t adding any new information to the path.

Brush strokes, simplified

At this point the best way to improve the my brush is to remove all the redundant points from our NSBezierPath. Since all the extra points don’t get in my way until mouse up happens, I’ll simply do some post processing on the NSBezierPath on mouse up. I’ll use the Ramer-Douglas-Peucker algorithm to identify and remove the redundant points. To demonstrate the effects of this algorithm, I’ll turn on the Simplify Path option, and draw another brush stroke:

You can see a big difference here in the number of points required to make up the path. The sample application outputs (using NSLog) how many points the path had before and after simplifying the path. In this case, the points went down from 170 to 15.

The Idea

The idea behind the Ramer-Douglas-Peucker algorithm is pretty simple. It takes a path and a threshold as parameters. I’ll show an example to demonstrate it. Let’s start with the following path:

I’ve numbered the points for easy reference. To start with I imagine a line between the end points, 1 and 5. I then measure the distance between each of the interior points (2, 3, 5) and the line made by points 1 and 5.

I take the greatest distance (the one between point 3 and my line) and compare it to the threshold passed in. If the distance exceeds the threshold, I have to subdivide the path and recurse. I split the path at the greatest distance (point 3 in this case), which gives me two paths: [1, 2, 3] and [3, 4, 5].

I repeat the process on [1, 2, 3] as my path:

Here my end points are 1 and 3, and my only interior point is 2. Like before I take the distance between point 2 and the line formed by 1 and 3, and compare it to the threshold passed in. In this case, the distance is less than threshold. Thus, I can say the interior points are all redundant and the path [1, 2, 3] can be represented by the endpoints 1 and 3.

Going back to the second recursion mentioned, I repeat the same process on [3, 4, 5]. In this case the distance between point 4 and the line between points 3 and 5 is less than the threshold. Because of that, I can represent the path [3, 4, 5] with just the end points 3 and 5. Thus, the final result is:

The Code

As you might expect the code for this algorithm is rather simple. It’s just one method (not counting the utility methods to access NSBezierPath data), which I’ve added as a category to NSBezierPath.

It takes a threshold as a parameter and returns the simplified path. It needs at least three points on the path before the algorithm will work.

- (NSBezierPath *) fb_simplify:(CGFloat)threshold
{
    if ( [self elementCount] <= 2 )
        return self;

Next it calculates the distance between the interior points and the line formed by the two end points. It remembers the largest distance and where in the path that point is.

    CGFloat maximumDistance = 0.0;
    NSUInteger maximumIndex = 0;

    // Find the point the furtherest away
    for (NSUInteger i = 1; i < ([self elementCount] - 1); i++) {
        CGFloat distance = FBDistancePointToLine([self fb_pointAtIndex:i], [self fb_pointAtIndex:0], [self fb_pointAtIndex:[self elementCount] - 1]);
        if ( distance > maximumDistance ) {
            maximumDistance = distance;
            maximumIndex = i;
        }
    }

FBDistancePointToLine() is a function I wrote that calculates the distance between a point and a line. fb_pointAtIndex is just a helper method that returns the point on the path at that index.

Now that it has the greatest distance, it checks to see if that distance is significant. If it is, then it recurses on itself, passing in the two halves split by the greatest distance. When the recursive calls return it joins the two results back into one, and returns those.

    if ( maximumDistance >= threshold ) {
        // The distance is too great to simplify, so recurse
        NSBezierPath *results1 = [[self fb_subpathWithRange:NSMakeRange(0, maximumIndex + 1)] fb_simplify:threshold];
        NSBezierPath *results2 = [[self fb_subpathWithRange:NSMakeRange(maximumIndex, [self elementCount] - maximumIndex)] fb_simplify:threshold];

        [results1 fb_appendPath:[results2 fb_subpathWithRange:NSMakeRange(1, [results2 elementCount] - 1)]];
        return results1;
    }

fb_subpathWithRange: is another utility method. It makes a copy of part of the path specified, and returns it. fb_appendPath appends one path to another, except it also will remove spurious move to’s and replace them with line to’s.

Finally, if the greatest distance isn’t significant, then all the interior points are redundant. In this case, just create a new path with the two end points.

    NSBezierPath *path = [NSBezierPath bezierPath];
    [path fb_copyAttributesFrom:self];
    [path moveToPoint:[self fb_pointAtIndex:0]];
    [path lineToPoint:[self fb_pointAtIndex:[self elementCount] - 1]];
    return path;
}

The only new utility method this time is fb_copyAttributesFrom:, which copies over attributes like caps, joins, and miters to the target path.

Curvy is better

So now I have a much simplified path representing my brush stroke. But my path is comprised of lines only, which are quite limited in representing anything other than a line. I’d like to have a way to represent curves. That way editing the path afterward would be even more powerful, plus I could reduce the number of total points on my path even more. Enter bezier curves.

Defining bezier curves is beyond the scope of this article. As far as this post is concerned they are a parametric curve defined by four points: two end points and two control points.

To further improve my brush stroke, I’m going to take my simplified path of lines, and fit a series of bezier curves to it. The algorithm for doing this is documented in Graphics Gems 1 in the article titled “An Algorithm for Automatically Fitting Digitized Curves” by Philip J. Schneider. Unfortunately, Graphics Gems is out of print. A Kindle version is available on Amazon, but it is 1) US$80 and 2) a poor quality scan. I would suggest buying the book used if you want a copy.

You can see the results of curve fitting by turning on the Fit Curve options in the Options menu and drawing a stroke. Here’s an example:

The black boxes are bezier curve control points. In this case using both path simplification and curve fitting reduced the number points from 197 to 7. Even better, bezier curves give the user more flexibility and power when it comes to editing the path.

Curve fitting overview

The curve fitting technique is somewhat involved and makes use of several different algorithms. I’ll only cover the methods unique to the algorithm and skip over a lot of details. That said, the sample code is complete and commented, so it can be used to fill in the details.

To start with, I’ll assume the function Q(t) represents a bezier curve that fits the points on my path. The parameter, t, ranges from 0 to 1, and Q(t) outputs x,y coordinates on my bezier curve. The first thing to do is calculate estimated values of t that match up to the points on my path. That is, Q(t[index]) should equal the point on my path at index.

After generating inputs for Q(t), the next step is to try to fit one bezier curve to the all the points on the path given the inputs. (I’ll describe the exact process later.) I’ll then compute how far the resulting bezier curve falls from the points on my path. If the curve is close enough, then I’m done.

If the bezier curve isn’t close enough to fit, I’ll see if it’s close enough that it makes sense to refine the inputs (t). If it is, I’ll repeatedly refine the input parameters (t) using Newton’s Method, until the resulting bezier curve fits sufficiently or I try more than four times.

If refining the input parameters doesn’t lead to a fit, it’s time to give up on one bezier curve, divide the path, and recurse. I’ll split the path into two at the point the bezier curve is furtherest from (i.e. where the greatest error is at). I’ll then recurse on the two halves, and then combine the two resulting curves into one bezier path for the final result.

The method fb_fitCubicToRange: in the NSBezierPath (FitCurve) category contains the code for the process described above if you want more detail.

Fitting a bezier curve to points

Remember that a bezier curve is defined by four points, like below.

Here points 1 and 4 are the end points and 2 and 3 are the control points. The orange lines just visually connect the control point with its corresponding end point. The blue curve is the bezier itself.

If we’re given a path of points to fit a curve to:

it’s easy to select the end points of the bezier curve; they’re simply the end points of the path (1 and 6 here). The direction of the control points relative to their end points is also simple to determine: simply compute the vector between the path end points and their nearest neighbor. In this case the direction of the left control point is the vector between points 1 and 2 in the path. The right control point direction is the vector between points 5 and 6. The only unknown in constructing our bezier curve is the distance between the control points and their respective end point.

Stated another way:

leftEndPoint = first point in path
rightEndPoint = last point in path
leftControlPoint = leftAlpha * leftTangent + leftEndPoint
rightControlPoint = rightAlpha * rightTangent + rightEndPoint

Where leftAlpha is the distance between the leftEndPoint and leftControlPoint, and rightAlpha is the distance between the rightEndPoint and the rightControlPoint. leftTangent and rightTangent are the unit vectors between the end points of the path and their closest neighbors.

By controlling the distance of the control points from their end points, I can affect the curve of the bezier. I want to chose distances (leftAlpha and rightAlpha) such that it best fits the points in the path. Formally stated, I want to minimize the squared errors as represented by:

S = SUM( (point[i] - Q(t[i])) ^ 2 )

Where point[i] is the point on the path at index i, t[i] is one of the estimated parameters I generated earlier, and Q is bezier curve. Remember that point[i] should be equal to Q(t[i]), assuming the bezier curve fits perfectly my points. Here I’m calculating how far each point on the bezier curve is off, squaring that, then adding it all up (squared errors). This is the error I calculate when I’m trying to determine if a bezier curve is close enough that I’m done. Right now though, I want to minimize S when calculating leftAlpha and rightAlpha.

Using the least squares approach I can write the equations I want to solve as:

d(S) / d(leftAlpha) = 0
d(S) / d(rightAlpha) = 0

Here d() is derivative, usually written as the Greek letter delta. S is the squared errors defined above.

At this point I do need to introduce the definition of a bezier curve:

Q(t) = SUM(V[i] * Bernstein[i](t))

Where i ranges between [0..3], and V is one of the points on the bezier curve. V[0] is the leftEndPoint, V[1] the leftControlPoint, V[2] the rightControlPoint, and V[3] the rightEndPoint. Berstein[i] is a polynomial that is highly regarded as boring for this discussion. (Look at the code if you really want to know.)

Now that I have Q defined, I can substitute it in the equation S, and then S into the two equations I want to solve. After a lot of mathematical voodoo and gymnastics (see the paper for all of that), I arrive at:

leftAlpha = det(X * C2) / det(C1 * C2)
rightAlpha = det(C1 * X) / det(C1 * C2)

Here det() is determinant, * is the dot product, and X, C1, and C2 are all 2×1 matrices defined below.

C1 = [SUM(A1[i] * A1[i]), SUM(A1[i] * A2[i])]
C2 = [SUM(A1[i] * A2[i]), SUM(A2[i] * A2[i])]
X = [SUM(partOfX * A1[i]), SUM(partOfX * A2[i])]

Where

partOfX = (points[i] - (leftEndPoint * Bernstein0(t[i]) + leftEndPoint * Bernstein1(t[i]) + rightEndPoint * Bernstein2(t[i]) + rightEndPoint * Bernstein3(t[i])))

And

A1[i] = leftTangent * Bernstein1(t[i])
A2[i] = rightTangent * Bernstein2(t[i])

If you’re interested in how this all plays out in code, check out the method fb_fitBezierInRange: in the NSBezierPath (FitCurve) category.

Calculating parameters (i.e. t)

The parameters (t) are useful for correlating the points on my path with the bezier curve I’m trying to fit. I know that t has to range from 0 to 1, and Q(t) is supposed to correspond to the points on my path. Q(0) should be the first point on my path, and Q(1) should be the last.

The initial estimate of t uses the chord length method. Ideally, t would be the length of curve from the left end point to the point corresponding to t, divided by the total length of the curve. However, the chord length method makes the assumption that a straight line is a reasonable estimate of a curve. So to estimate t, I measure the length of the line segments from the left end point to the point corresponding to t, then divide that by the length of all the line segments.

You can inspect the implementation of this in the fb_estimateParametersUsingChordLengthMethodInRange: method.

If my initial estimate proves to be poor, I can further refine it using Newton’s Method. Newton’s Method says I can refine each t value by:

t = t - f(t) / f'(t)

In my case

f(t) = (Q(t) - point) * Q'(t) = 0

Here (Q(t) –point) is the vector from a point on the bezier curve to the corresponding point on my path. Q’(t) is the first derivative, which is tangent to the bezier curve, Q, at t. (Q(t) –point) is orthogonal to Q’(t), which means the dot product of the two is zero.

Based on that, f’(t) is

f'(t) = (Q(t) - point) * Q''(t) + Q'(t) * Q'(t)

The NewtonsMethod() function in NSBezierPath+FitCurve.m implements this.

Conclusion

Although I skipped over a lot of detail when it came to curve fitting, hopefully this post has been helpful in understanding how it works, in addition to explaining the vector brush. For the details that I skipped over, the code should fill in the blanks. The vector brush is a fun tool to play with and the curve fitting algorithm has other applications too.

The talk I’m working on for NSConference 2010 involves a decent amount of OpenCL kernel code. Originally, I thought I would develop the kernel code the same way I develop Core Image kernel code: build the kernel in Quartz Composer and then copy paste the code into Xcode when I got it working.

Unfortunately, I’ve not had much luck with Quartz Composer in way of meaningful compiler errors. Sometimes it returns good errors, sometimes inscrutable ones.

Composer: Wait, wait, I remember this… it’s COBOL, right?

However, I’ve found debugging OpenCL kernels to be much easier thanks to the invention of a function I like to call “printf.” If you run your kernel on the CPU, then you can print out values just like in C. With debugging solved, I just needed to figure out how to find compiler errors without having to run my code.

Unlike Core Image, OpenCL actually requires you to compile your kernel code explicitly before using it. The API’s required to do this will return nice compiler error messages and everything. The obvious thing to do would be wrap up these API’s in a command line tool and invoke the tool from Xcode, which is what I did.

The Code

You can download the Xcode project for clc, the OpenCL Compiler here. It requires Mac OS X 10.6 Snow Leopard and the associated Xcode tools. To install, just build the project and copy the resulting binary into your path somewhere. I used ~/bin.

Most of the code is self explanatory, with the possible exception of the output. Unlike most compilers, clc doesn’t output object code because the host and runtime CPU/GPU’s could easily be different. It could simply copy the source code as is for the output, but that was a little too obvious for my tastes. Instead clc compresses the source code and stuffs it into a binary plist. It has the slight benefit of potentially being smaller on disk, and making your source code negligibly less accessible to prying eyes, if you’re into that sort of thing.

There are definite possibilities for improvement. For example, there could be an option to encrypt the source code to be more “secure.” Or it could store the binary code generated by the host machine in the output on the chance that the host and runtime machines have the same hardware.

Setting up Xcode

To use clc, you’ll need to set up a build rule in your app’s target settings to run all OpenCL source files through it. Selecting the menu item Project > Edit Active Target, and then selecting the Rules tab, should land you here:

Add another rule, set it to process OpenCL source files using a Custom script. For the custom script enter:

~/bin/clc ${INPUT_FILE_PATH} -o ${TARGET_BUILD_DIR}/${PRODUCT_NAME}.app/Contents/Resources/${INPUT_FILE_BASE}.clar

Finally, you’ll need to tell Xcode where you’re putting the output file, which is:

${TARGET_BUILD_DIR}/${PRODUCT_NAME}.app/Contents/Resources/${INPUT_FILE_BASE}.clar

By default, Xcode won’t put OpenCL source files (.cl) into the target, meaning they won’t get compiled. For each of your OpenCL source files
you’ll need to explicitly add them to your target. There are several ways to do this, but the easiest is probably selecting all of them, and doing a Get Info (File > Get Info). Switch to the Targets tab and check the target they should be compiled into.

Runtime Code

At runtime, it’s pretty easy to retrieve the original OpenCL source code using the + (NSString *) openCLSourceWithData:(NSData *)data error:(NSError **)error; method on ONOpenCLArchive. However, there are a couple of convenience methods on NSBundle that makes retrieving the kernel easier. For example:

#import "ONOpenCLArchive.h"

NSString *kernelSource = [[NSBundle mainBundle] openCLResource:@"MyKernel"];

That’s pretty much all there is to it.

Conclusion

Although not ground breaking, this little tool has certainly been helpful to me by finding compiler errors at compile time instead of runtime. Hopefully it will be useful to other people as well.