Safe from the Losing Fight

I’ve been meaning to write about some of the major problems that I have with the App Store, both the Mac and iOS varieties. But honestly, I don’t have a whole lot to add to what Wil Shipley and Craig Hockenberry have already said. Instead, I’ll link to the bugs I’ve written up, and encourage you to do the same.

• The App Stores need to support upgrade pricing. rdar://11131356 or Open Radar

• The App Stores need to support free trials. rdar://11133210 or Open Radar

• The App Stores need to support tracking statistics. rdar://11133330 or Open Radar

• The App Stores need better discoverability of apps. rdar://11133573 or Open Radar

I know there’s been a lot of pessimism about writing up Radars lately, including from yours truly. But the truth is filing bugs is the only official way Apple will listen, so the pragmatic side of me wins out. It’s not that I necessarily think filing bugs will cause a change, but it’s the only possible way of affecting changing that’s been given to me.

Previously, I covered how to find the intersections between two bezier curves and gave a conceptual overview of how to perform boolean operations on bezier paths. In this final installment I’ll present the algorithm used to implement the boolean operations.

Overview

The algorithm that I show here is based on the algorithm presented in “Efficient clipping of arbitrary polygons” by Günther Greiner and Kai Hormann. My algorithm is adapted to work on closed bezier paths (instead of polygons), handle nonintersecting (sub)paths, and handle intersections between fill paths and hole paths.

As before the full source code is available on Bitbucket, and it’s licensed under the MIT license. If you want to follow along, the majority of the algorithms described are implemented in the FBBezierGraph class.

Data Structures

My algorithm, like Greiner-Hormann’s, uses several data structures. The primary is FBBezierGraph. Think of FBBezierGraph as an expanded version of NSBezierPath that can be annotated with where intersections happen. FBBezierGraph contains FBBezierContours, which are just closed subpaths. Anytime I see a moveto in a NSBezierPath, that’s a new contour. FBBezierContours in turn contain FBContourEdges, which are mainly wrappers around a FBBezierCurve. They represent one cubic bezier curve, and can also hold FBEdgeCrossings. Each FBEdgeCrossing represents a location where another edge crosses this edge.

By breaking a NSBezierPath out into all these separate structures, it makes it easier to process. Contours need to be dealt with one at a time, and I need a way to keep track of where the intersections happen. The basic flow is to convert my NSBezierPath into a FBBezierGraph, perform the boolean operation, then convert it back to a NSBezierPath. FBBezierGraph handles both sides of the conversion.

Basic Algorithm

The basic algorithm for union, intersect, and difference are very similar. In fact, there’s only one step that’s all that different between the three. The basic steps are:

1. Find all the intersections where the edges actually cross, and insert FBEdgeCrossings into both FBBezierGraphs at those locations.

2. Handle all the intersecting contours.

   • Walk each contour and mark the entry and exit into the section I want to output to the final result.

   • Walk each contour and output the final contours by following the entry and exit directions marked in the previous step.

3. Handle all the nonintersecting contours.

Step three is the only step that is very different between the operations. Step two is identical except for if we mark the inside or outside section.

The above algorithm only applies to union, intersect, and difference. On the other hand, the entire implementation for exclusive or is:

- (FBBezierGraph *) xorWithBezierGraph:(FBBezierGraph *)graph
{
    FBBezierGraph *allParts = [self unionWithBezierGraph:graph];
    FBBezierGraph *intersectingParts = [self intersectWithBezierGraph:graph];
    return [allParts differenceWithBezierGraph:intersectingParts];
}

As I’ve mentioned previously, exclusive or is implemented in terms of union, intersect and difference. I’ll now ignore exclusive or for the rest of the post.

Finding Crossings

For all three operations I start the same way: finding all the intersections where the edges cross. I do this by simply walking each edge of the subject bezier graph and intersecting them with the edges of the clipping graph. I don’t look for self intersections. I insert a FBEdgeCrossing into each bezier graph for each intersection, and point the crossings at each other so I can easily jump between graphs at crossings. You can find the code for this in the insertCrossingsWithBezierGraph: method.

There are a couple of things I have to look out for when determining if two edges actually cross at an intersection. One possibility is that the two edges are tangent at the intersection, and don’t cross. That is straightforward to detect; I compute the tangent for both curves at the intersection point, and see if they’re parallel. If they are, then they are tangent at that point.

The more involved case is when the intersection happens at the end point of one or both of the edges. If an intersection happens in the interior of two curves, and it’s not tangent, then I know the edges actually cross. But suppose I encounter the following intersection:

I don’t know if the two contours cross or not just by looking at these two edges alone. I need to look at the next edge. There are two basic possibilities:

Either the contours cross at the intersection, or they don’t (I consider going coincident to be not crossing). I use the tangents at the intersection point to determine if the contours actually cross or not. The tangents for the above examples look something like:

I then compute the angles of the tangents by computing the polar coordinates. If the contours cross, the angles will cross as well. The method doesEdge:crossEdge:atIntersection: implements the crossing check.

When finding crossings I have to be wary of one additional problem caused by intersections at end points. Since the end of one edge is the start of the next, an intersection at the end point will be found on both edges, resulting in duplicate crossings. So when I’m done finding all the crossings, I’ll go through the crossings I found and remove the duplicates.

Intersecting Contours

I take the processing of intersecting contours in two steps: marking which sections (inside or outside) of each contour to output, and then creating a new bezier graph containing those sections. The code for doing this for all three boolean operations is:

    [self markCrossingsAsEntryOrExitWithBezierGraph:graph markInside:NO];
    [graph markCrossingsAsEntryOrExitWithBezierGraph:self markInside:NO];

    FBBezierGraph *result = [self bezierGraphFromIntersections];

This is the code from the union operation. The code for the intersect and difference operations are identical except for the values passed in to the markInside parameter. Intersect passes YES for both self and graph, while difference passes NO for self and YES for graph (marking the outside of self and inside of graph).

When I mark the crossings as entry or exit, I go one contour at a time and mark the entries and exits relative to the other contour crossing it:

- (void) markCrossingsAsEntryOrExitWithBezierGraph:(FBBezierGraph *)otherGraph markInside:(BOOL)markInside
{
    for (FBBezierContour *contour in self.contours) {
        NSArray *intersectingContours = contour.intersectingContours;
        for (FBBezierContour *otherContour in intersectingContours) {
            if ( otherContour.inside == FBContourInsideHole )
                [contour markCrossingsAsEntryOrExitWithContour:otherContour markInside:!markInside];
            else
                [contour markCrossingsAsEntryOrExitWithContour:otherContour markInside:markInside];
        }
    }
}

Above I check to see if the other contour I’m intersecting with is a hole or not. As I talked about in the previous post, if the other contour is a hole, then I want to mark the opposite section that I normally would for this operation.

The method markCrossingsAsEntryOrExitWithContour:markInside: does the actual marking of crossings as entry or exit. The pseudocode for marking entries and exists:

1. I pick a point on the contour to start with.

2. I determine if the point lies inside or outside the other contour, using the even odd rule.

3. Using the markInside parameter and if the start point is inside or outside, I determine if the start point is in the section I want to output or not.

   1. If the start point is in the right section already, the next crossing will be an exit, so assign isNextCrossingAnEntry = NO.

   2. If the start point is not in the section I want to output, the next crossing will be an entry, so I assign isNextCrossingAnEntry = YES.

4. For each crossing on the contour (starting with my start point and proceeding in order):

   1. Assign the crossing’s property isEntry = isNextCrossingAnEntry.

   2. Toggle the value of isNextCrossingAnEntry.

The only tricky part of this is choosing a good start point. I don’t want a start point that is ambiguous, like one that is on the other contour.

After I’m done marking all the crossings as entry or exit, I need to build the final contours. The algorithm for that is:

1. While there are unprocessed crossings do:

   1. I find the first unprocessed crossing on the bezier graph.

   2. I create a new contour.

   3. While the current crossing hasn’t be processed do:

      1. If the crossing is an entry, I move forward through the contour adding the edges (or edge segment if there’s a crossing) until I encounter the next crossing.

      2. Else the crossing is an exit, and I move backwards through the contour, adding edges (or segments) until I encounter the next crossing.

      3. I switch to the other bezier graph by setting the current crossing to it’s counterpart.

   4. I add the new contour to the final bezier graph.

And now I’m done processing all the intersecting contours.

Nonintersecting Contours

The final part of a boolean operation is dealing with the nonintersecting contours. This is where the various boolean operations differ the most. I start with the list of contours that don’t intersect anything.

For the union operation, I start out optimistically and assume they’ll all end up in the final result. I then walk both bezier graph’s nonintersecting contours and see if an individual contour is inside (as defined by the even odd rule) the opposite bezier graph. If it is, I know it’s redundant and I remove it from the final contours.

The code looks something like:

    for (FBBezierContour *ourContour in ourNonintersectingContours) {
        if ( [graph containsContour:ourContour] )
            [finalNonintersectingContours removeObject:ourContour];
    }
    for (FBBezierContour *theirContour in theirNonintersectinContours) {
        if ( [self containsContour:theirContour] )
            [finalNonintersectingContours removeObject:theirContour];
    }

Intersect is more or less the opposite of union. I start by assuming none of the nonintersecting contours from either bezier graph will make it. I then walk all the nonintersecting contours and see if the opposite bezier graph contains them. If the opposite graph does, then there is overlap, and the overlap is the contour being contained.

A simplified version of the code for intersect is:

    for (FBBezierContour *ourContour in ourNonintersectingContours) {
        if ( graph containsContour:ourContour] )
            [finalNonintersectingContours addObject:ourContour];
    }
    for (FBBezierContour *theirContour in theirNonintersectinContours) {
        if ( [self containsContour:theirContour] )
            [finalNonintersectingContours addObject:theirContour];
    }

I start computing the difference for nonintersecting contours by assuming none will make it into the final result. I then walk the nonintersecting contours for the subject bezier graph. If they are not contained by (and thus not subtracted away) the clipping bezier graph, I add them to the final contours. Next I walk the nonintersecting contours for the clipping bezier graph. If they are contained by the subject bezier graph, that means they cut a hole in the subject, so I add them to final contours.

The code looks kind of like:

    for (FBBezierContour *ourContour in ourNonintersectingContours) {
        if ( ![graph containsContour:ourContour] )
            [finalNonintersectingContours addObject:ourContour];
    }
    for (FBBezierContour *theirContour in theirNonintersectinContours) {
        if ( [self containsContour:theirContour] )
            [finalNonintersectingContours addObject:theirContour]; // add it as a hole
    }

And with that I’m done. I have the final intersecting and nonintersecting contours and can convert the bezier graph back into a NSBezierPath.

Contour Containment Issues

In the previous section, I skipped over the implementation of the containsContour: method despite the fact it gave me fits in practice. In theory it should be easy to implement: I pick a point on the contour and use the even odd rule to see if the point is inside the other bezier graph or not. Unfortunately there are two situations which make it not as simple as I’d hoped.

The first problem is easiest seen:

Does the blue contour contain the red? In both cases the even odd rule returns one intersection, indicating that it does. However, just by looking at it, I can tell that in the diagram on the right, it doesn’t. The problem is the ray passes through an edge where both contours coincide.

The second problem is show below:

This one is a bit more subtle. Notice that the ray I’m using to determine even or odd intersects where two edges meet. This means I’ll find two intersections (one for each edge) instead of just one, and I’ll think the red square is outside the blue circle.

My solution is somewhat brute force. I actually ended up casting a full line through the entire contour, instead of just one side, in order to increase my chances of getting a useful ray. I also alternate between horizontal and vertical lines, and I loop until I get a line that is unambiguous. There is more code dedicated to this operation that I like. There is probably a better way to do this.

Conclusion

I took on this project mainly for my own benefit, so I could learn how this works. But hopefully you’ve learned something useful too amidst all my struggling with this.

I have tried to test the sample code the best I could. You can check out all the test cases under the “Shapes” menu in the sample application. However, I’ve undoubtedly missed or left out edge cases which will cause the code to fail. If you decide to use this code in a commercial application: test, test, test. If you do find a case my code doesn’t handle, I’d like to hear about. That said, the code is provided as is, and I’m not guaranteeing any support for it.

In my last post I showed how to find the intersection points between two bezier curves. While interesting, it’s merely a stop on the way to implementing boolean operations for bezier paths. This time I’ll show how to conceptually perform the four common boolean operations: union, intersect, difference, and exclusive or. I’ll cover the actual algorithms for implementing the four operations in the next post.

Conceptually Speaking

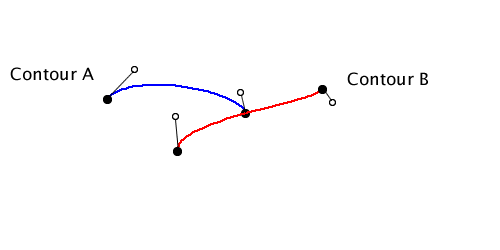
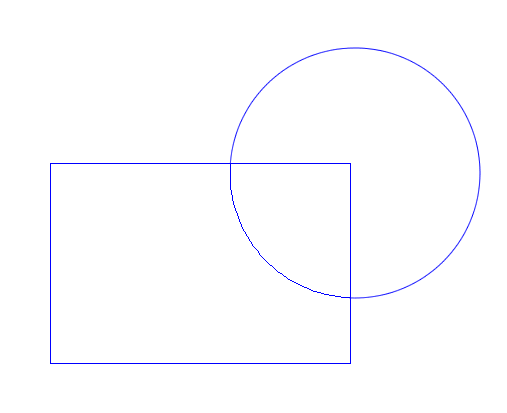
I think it’s helpful to start out with a simple case and see how this will work conceptually. I’ll start with the following example:

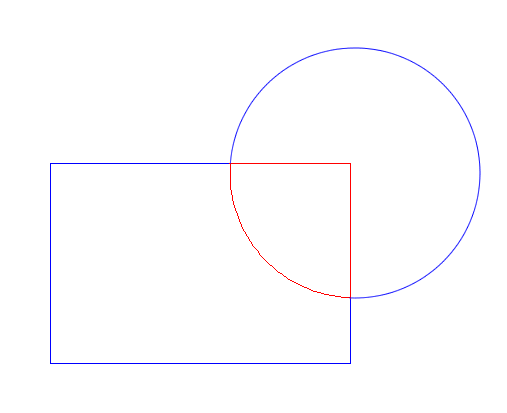
Here I have a rectangle and circle overlapping. The intersections have already been calculated and circled in green. Now I consider the shapes as wireframes:

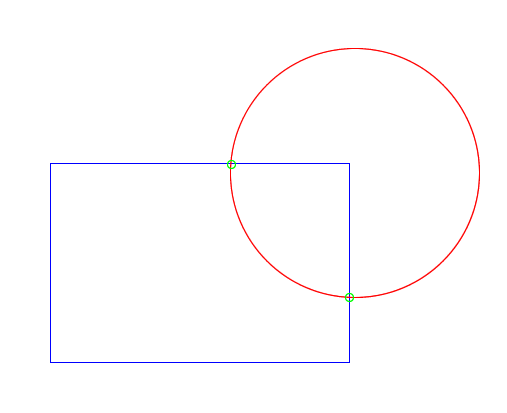
In my head, I divide up each path into sections based on the intersection points. There are two kinds of sections: one that is outside the other path, and one that is inside the other path. Performing a boolean operation is just a matter of picking the correct section from each path.

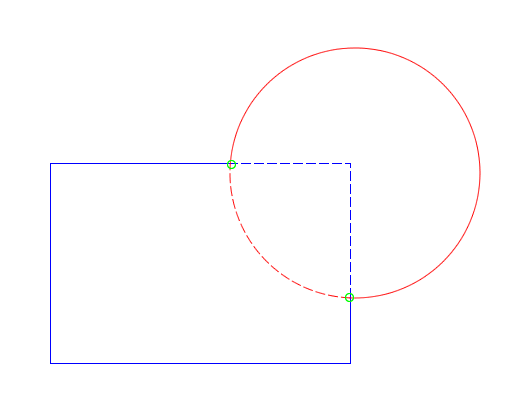
Here I’ve used a dashed style to mark which parts of the path are inside of the other path. Once I’ve separated the paths into the inside and outside parts, it’s easy to perform the boolean operations conceptually.

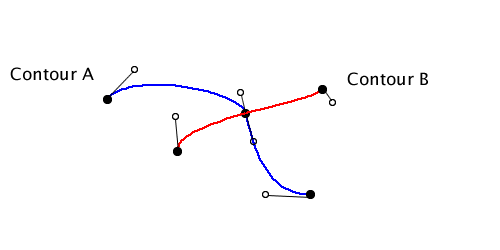
A union is a logical or, so I want all the outside sections:

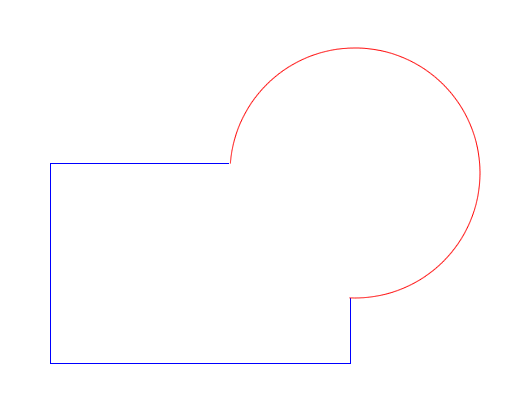
The intersect operation is a logical and, so I just want the inside sections:

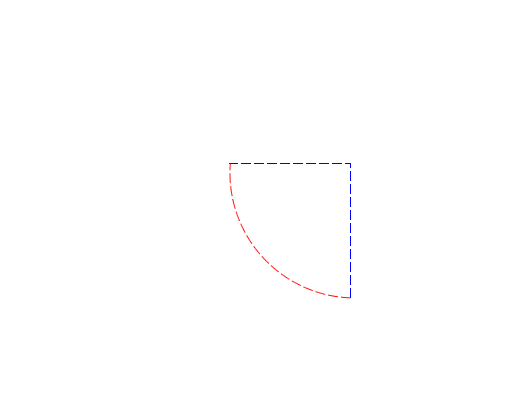
Difference is where I take a path and remove the parts that intersect with the other path. For that I want the outside sections of the subject (the rectangle), and the inside sections of the clip (the circle):

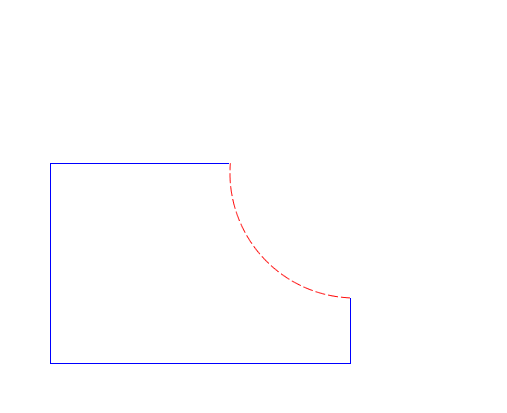
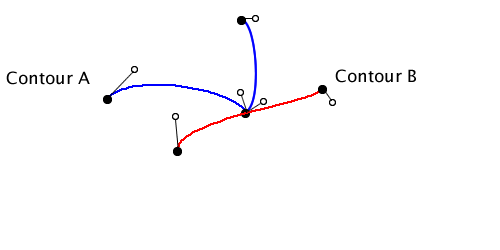
For now I’m going to ignore logical exclusive or because it requires properly handling subpaths and holes, which I’m not ready to talk about just yet. However I will say that exclusive or isn’t a primitive like the other operations, but is defined in terms of union, intersect, and difference. Specifically A Xor B is defined as (A Union B) Difference (A Intersect B).

Where is inside?

Before I go any further, I need to define what it means for a point or path to be “inside” of another. The previous examples were simple and just by eyeing them I could tell if a point or path section was inside or not. However, I’ll need something more robust for more complex operations.

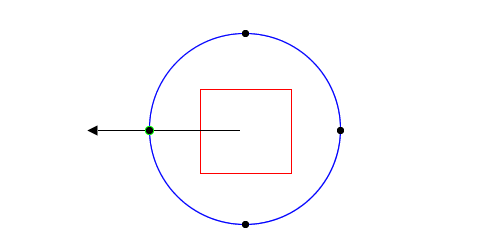
Traditionally there are two ways to determine if a given point is inside a closed path or not. First, there’s the winding rule. I count how many times the path winds around the given point. If it’s more than 0, then the point is inside the path. This is default way NSBezierPath determines if a point is inside a path or not.

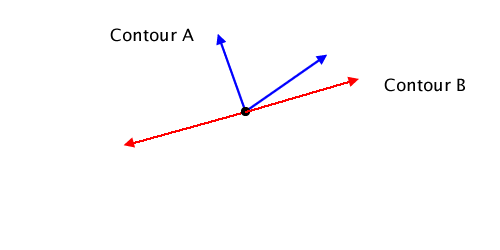
The second way is the even odd rule, which is the one I use in my implementation and for the rest of this post. I draw a ray from the given point to outside the bounds of the path. I then count how many times the ray intersects the path. If it is an odd number of times, then the point is inside the path. If even, it’s outside.

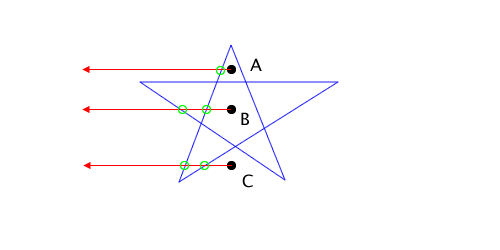
The star in the above diagram is one closed path. I’ve added three points A, B, and C to various places in the diagram, and applied the even odd rule to determine if they’re inside the star or not. The red arrow represents the ray I drew from the point to the outside of the path. (It doesn’t have to be a horizontal ray, it can go in any direction.) The ray from point A crosses the path exactly once, an odd number of times meaning it falls inside the star. The ray from point C crosses the path twice (even) so it is outside the star. Just by looking at the diagram it’s easy to see that A is inside and C is outside.

However, when I cast a ray from point B it also intersects with the star an even number of times, meaning it lies outside the path. This isn’t necessarily intuitive by looking at the diagram, but it is important for allowing holes in a path.

Both the winding rule and the even odd rule are called fill rules, because their main purpose is to determine which parts of a path are filled. Using the even odd rule the star above would be filled like:

The star has a hole in the middle. However, this isn’t the only way holes can be introduced to a path. Holes can be formed by unconnected subpaths. For example:

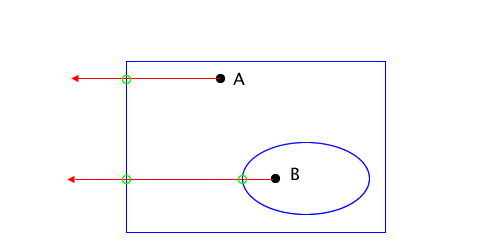
Here both the rectangle and ellipse are part of the same path; they’re just disjoint subpaths. As with the star, the same even odd rule applies meaning point A is inside the path, but B is not. The rectangle would be filled, except for the area the ellipse defines.

Nonintersecting Paths

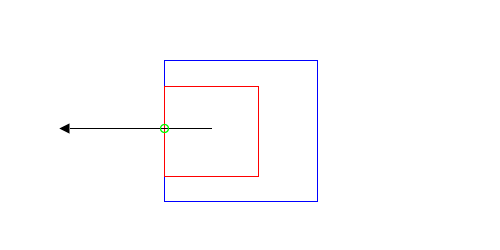
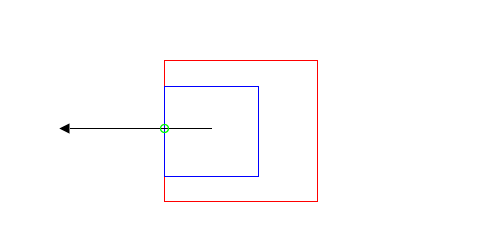
Now that I’m done with that detour into fill rules and holes, I want to get back to boolean operations between two paths. I started with how to compute the results of a boolean operation if the two paths intersect, but what if the paths don’t intersect? There are two non-intersecting states I care about: when one path contains the other, and when the two paths lie outside of each other. I’ll start with two examples illustrating both of these states:

Contained
Disjoint

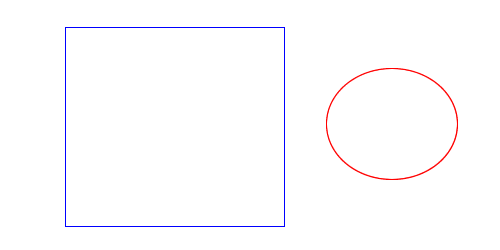
For the union operation, I want to eliminate any paths that are contained by another path. However a path is only contained by another if it falls inside the filled region as defined by the even odd rule. If the two paths lie outside of each other, the result of a union is both of them. So union-ing my two examples would result in:

Contained
Disjoint

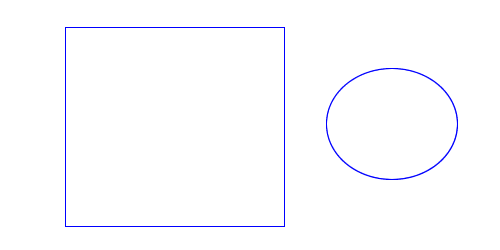
Intersect, being the logical and, eliminates any area where both paths aren’t filled. In the case where one path contains another, the contained path is the one where both paths are filled. If the two paths don’t overlap in any way, then the result is nil.

Contained
Disjoint	(nil)

Difference starts with one path, which I’ll call A, and removes all the places that another path, B, fills. In the case of containment which path contains the other matters. If I’m computing A –B, and A contains B, then I’ll add B as a hole subpath to path A. If B contains A, then all of A subtracted away, and I’m left with nil. If the paths don’t overlap, and I’m computing A –B, then nothing changes and I’m left with A as the result.

For this example, assume the blue rectangle is A and the red ellipse is B.

Contained (A –B)
Contained (B –A)	(nil)
Disjoint (A –B)
Disjoint (B –A)

Intersecting Holes

Now that I’ve discovered holes, it’s time to see what happens when a path intersects with one. The process is the same as performing the operations on two normal paths, except which section (inside or outside) I chose to go in the result. I’ll start with a simple example:

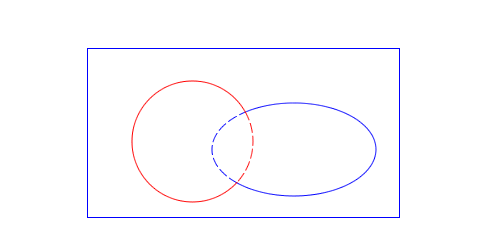
In the above diagram, the blue rectangle and ellipse form one path, with the ellipse being a hole. The red circle forms the second path. As before the inside sections of the intersecting (sub)paths are shown in a dashed style.

For a union I’d normally choose the outside sections of both paths. However since the blue ellipse is a hole, the red circle should intrude into it. So I would pick the inside of the red circle and the outside of the blue ellipse. More generally, I would always pick the outside section of a path, unless the other path was a hole, then I’d pick the inside section. The union result would be:

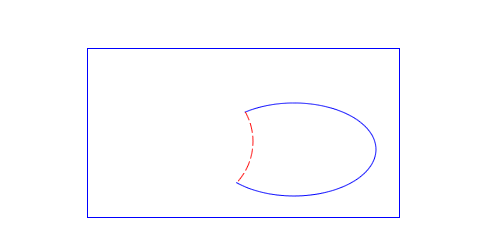
Note that since the blue rectangle is nonintersecting, it passes straight through to the result. (See the previous section about nonintersecting paths.)

Intersect would normally choose the inside sections of each path. However, both paths clearly don’t exist inside of a hole. So when I choose which section to output for a given path, if the other path is a hole I’ll pick the outside section instead of the usual inside section. Here are the results of the intersect on these two paths:

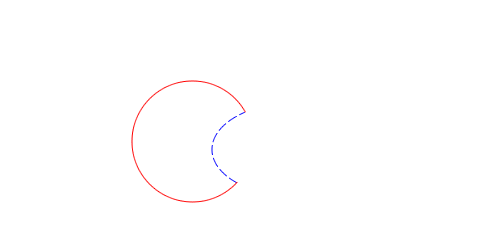
In the intersect I remove the blue rectangle entirely, since it is a nonintersecting (sub)path.

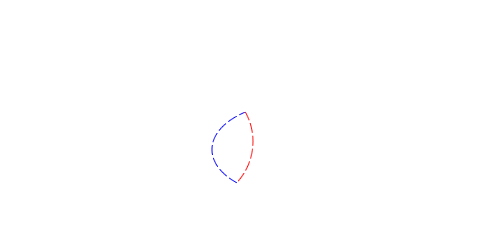
In a difference operation the order of the operands matters, so I’ll take each direction separately. If I subtract the red (path B) from the blue (path A), normally I would chose the outside of A and the inside of B. However, just from eyeballing the paths I can tell that I should take the outside of B. When choosing which section to output for B, I look to see if A is a hole. If it is, I take the outside of B instead the inside, resulting in:

To compute B –A, I would usually pick the outside of B and the inside of A. But since A is a hole, I choose the inside of B, with the following results:

By now I’ve noticed a pattern for all the boolean operations. I choose the section of a path I normally would for that operation, unless the intersecting path is a hole. If it is I pick the opposite section than I normally would.

Exclusive Or Revisited

Now that I know about holes and how to perform union, intersect and difference on non-intersecting paths I can tackle exclusive or. I’ll return to the first example:

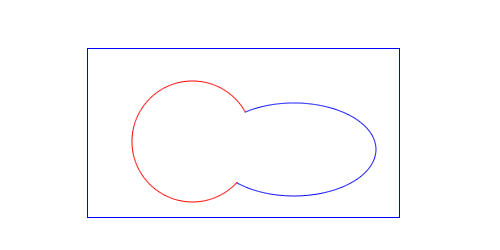
Now I take both the union and the intersect of both these paths, then subtract the intersect from the union for the final result. Below is the intermediate step after the union and intersect have been computed, but before the difference.

The union is in blue, and the intersect is in red. This diagram is a good illustration of an edge case. Technically there are two intersections between these two paths where the original rectangle and ellipse meet. However the two paths don’t fully cross each other at these intersections, they just meet at a point. Because of this, I ignore them. This holds true for any intersection: if the paths don’t cross each other then I ignore it for the purposes of boolean operations.

Since there are no crossing intersections, taking the difference happens between two paths that don’t intersect, and I fall back to those rules. The result of the xor:

There are two subpaths in the result: the union and the intersect subpaths. The interior subpath from the intersect thus forms a hole. If the result were filled, it would be:

Conclusion

All these pieces come together to be able to handle boolean operations for complex paths. First I handle all the intersecting subpaths as described, whether they are fill or hole. Then I process all nonintersecting subpaths, ignoring any intersecting subpaths for those computations.

This time I focused strictly on how to perform the boolean operations conceptually, based on the assumption I could find all the intersections. I covered how to think about paths as inside and outside sections, and how to perform boolean operations based on picking the correct section from each path. This is an important foundation for next time, when I’ll dig into the algorithms that actually implement these boolean operations.